The Lorentz force law is
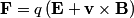 Initially, 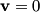 , so the second term inside the parenthesis is , so the second term inside the parenthesis is 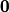 . So, at . So, at 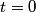 , the particle experiences a force in the direction of the electric field, which gives the particle a velocity in the direction of the electric field. Since , the particle experiences a force in the direction of the electric field, which gives the particle a velocity in the direction of the electric field. Since 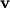 and and 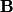 are parallel, the second term inside the parenthesis is still are parallel, the second term inside the parenthesis is still 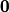 . So, the particle will continue to move in a straight line and not experience any magnetic force. Therefore, answer (E) is correct. . So, the particle will continue to move in a straight line and not experience any magnetic force. Therefore, answer (E) is correct. |